Multiplication Clusters
There are numerous ways to decompose one of the factors in a multiplication problem in order to make a "cluster" (group) of smaller problems which combine to solve the larger problem. Students decompose one of the factors while keeping the other factor constant. Below, Allison's work shows that 32 can be decomposed into 30 and 2 while 21 remains constant, so that 30 x 21 (30 "groups of" 21) and 2 x 21 can combi ne to solve for 32 x 21. Each of these smaller problems usually can be calculated using mental math, since at least one of the factors is either a one-digit number or a multiple of 10. 30 x 21 can be solved by knowing that a "related problem", 3 x 21, equals 63. Therefore, 30 x 21 equals 630. She also shows, in her second example, that 21 can be decomposed into 20 + 1 so
ne to solve for 32 x 21. Each of these smaller problems usually can be calculated using mental math, since at least one of the factors is either a one-digit number or a multiple of 10. 30 x 21 can be solved by knowing that a "related problem", 3 x 21, equals 63. Therefore, 30 x 21 equals 630. She also shows, in her second example, that 21 can be decomposed into 20 + 1 so  that mental math can be used to find 21 groups of 32.
that mental math can be used to find 21 groups of 32.
There are numerous ways to decompose one of the factors in a multiplication problem in order to make a "cluster" (group) of smaller problems which combine to solve the larger problem. Students decompose one of the factors while keeping the other factor constant. Below, Allison's work shows that 32 can be decomposed into 30 and 2 while 21 remains constant, so that 30 x 21 (30 "groups of" 21) and 2 x 21 can combi
 ne to solve for 32 x 21. Each of these smaller problems usually can be calculated using mental math, since at least one of the factors is either a one-digit number or a multiple of 10. 30 x 21 can be solved by knowing that a "related problem", 3 x 21, equals 63. Therefore, 30 x 21 equals 630. She also shows, in her second example, that 21 can be decomposed into 20 + 1 so
ne to solve for 32 x 21. Each of these smaller problems usually can be calculated using mental math, since at least one of the factors is either a one-digit number or a multiple of 10. 30 x 21 can be solved by knowing that a "related problem", 3 x 21, equals 63. Therefore, 30 x 21 equals 630. She also shows, in her second example, that 21 can be decomposed into 20 + 1 so  that mental math can be used to find 21 groups of 32.
that mental math can be used to find 21 groups of 32. Generic Rectangle Alexis shows her understanding of how this model is used when both factors are decomposed (32 into 30 + 2 and 21 into 20 + 1). Each cell in the rectangle contains the product of the row and column  number. Once these are calculated (primarily through the use of mental math strategies due to the simplistic representation of each number as either a one-digit number or multiple of 10), all partial products are combined together to achieve the final product for 32 x 21.
number. Once these are calculated (primarily through the use of mental math strategies due to the simplistic representation of each number as either a one-digit number or multiple of 10), all partial products are combined together to achieve the final product for 32 x 21.
 number. Once these are calculated (primarily through the use of mental math strategies due to the simplistic representation of each number as either a one-digit number or multiple of 10), all partial products are combined together to achieve the final product for 32 x 21.
number. Once these are calculated (primarily through the use of mental math strategies due to the simplistic representation of each number as either a one-digit number or multiple of 10), all partial products are combined together to achieve the final product for 32 x 21. 
Separate Listing of Partial Products for Traditional Algorithm
Mateo shows his understanding of how the traditional algorithm works in the order that he lists the partial products for each step in the algorithm process for multiplying two two-digit numbers. Instead of regrouping, he lists partial products separately, and then combines all four together to get the final product for 32 x 21. Can you see a connection between Mateo's partial products and Alexis' partial products in the above example?
Jaeda shows an understanding of the procedures for using the traditional algorithm for multiplying two-digit numbers. The traditional algorithm is typically seen as an "efficient" way of finding the product of two factors, and we encourage students to use this method as long as they have a conceptual understanding of what it means to multiply two digit numbers and that they have another strategy of finding the product of two numbers (such as one of the strategies showcased in the preceding examples).

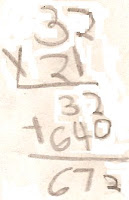
5 comments:
Way to go Jaeda! That is awesome. We are so proud of you!
~Heather (Jaeda's stepmom)
they are awesome at math.
rp#16-heather
Hey girl,
I am so proud of the work you and your classmates are doing. You are learning so much and still having fun.
Love,
Grandmama Reeves, GA
As always Alexis makes me proud! All these kids are so smart I know that FCAT will be a BREEZE for them!
Laura Ancelin
It is nice to see that students are mathematical thinkers rather than just procedural robots. You are teaching number sense, mental math, and connections rather than just showing them a procedure for solving. Your students will be prepared for more advanced mathematics.
Post a Comment