Grouping Fractions According to Landmarks

After creating 40 fraction cards in class, we organized them into groups based on connections we made about them after analyzing relationships between numerators and their denominators. By doing this, we were able to make many generalizations about fractions.

#1- Fractions that have "0" as a numerator equal 0. (Zero parts are named, or shaded.)

#2- Fractions that have a numerator which is exactly one-half of its denominator equal 1/2. 2 is half of 4, so 2/4 = 1/2.

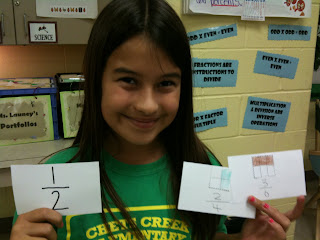We also added to this observation by saying that since the numerator is half the denominator, IF WE DOUBLE THE NUMERATOR IT WILL EQUAL THE DENOMINATOR.

#3- Fractions that have a numerator equal to its denominator equal 1 whole. If 8 out of 8 parts are shaded, the whole is shaded, therefore, 8/8 = 1 whole.
Those first three groupings were easy to make, as you can imagine. When placing fractions BETWEEN LANDMARKS, though, our generalizations became more advanced!

Here we have two fractions that fall BETWEEN 0 and 1/2. In this case, the numerators are "less than half" of the denominators BUT "greater than zero".

For example, with 2/6, half of 6 is 3, but fewer than 3 parts (only 2) are shaded; therefore, the fraction is LESS than 1/2.

Here we have three fractions that fall BETWEEN 1/2 and 1 whole. In this case, the numerators are "more than half" but "less than equal to" to denominator.

For example, half of 8 is 4, therefor 4/8 = 1/2.

If I have the fraction 5/8, since 5 is more than 4 (half the denominator), then the fraction is greater than 1/2.

We are now beginning to explore decimal and percent equivalents for fractions in class- new, powerful strategies to add to our tool belts when we compare fractions! Math is FUN when there are multiple ways to solve problems and justify our reasonings!

What do you think about fractions, decimals, and percents? Leave a comment!

Love,

Mrs. Phillips