#1- Fractions that have "0" as a numerator equal 0. (Zero parts are named, or shaded.)


#2- Fractions that have a numerator which is exactly one-half of its denominator equal 1/2. 2 is half of 4, so 2/4 = 1/2.
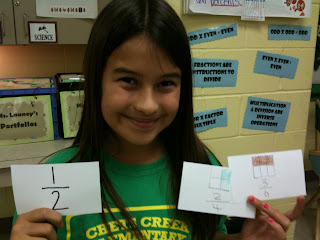 We also added to this observation by saying that since the numerator is half the denominator, IF WE DOUBLE THE NUMERATOR IT WILL EQUAL THE DENOMINATOR.
We also added to this observation by saying that since the numerator is half the denominator, IF WE DOUBLE THE NUMERATOR IT WILL EQUAL THE DENOMINATOR. #3- Fractions that have a numerator equal to its denominator equal 1 whole. If 8 out of 8 parts are shaded, the whole is shaded, therefore, 8/8 = 1 whole.
 Those first three groupings were easy to make, as you can imagine. When placing fractions BETWEEN LANDMARKS, though, our generalizations became more advanced!
Those first three groupings were easy to make, as you can imagine. When placing fractions BETWEEN LANDMARKS, though, our generalizations became more advanced!
 Those first three groupings were easy to make, as you can imagine. When placing fractions BETWEEN LANDMARKS, though, our generalizations became more advanced!
Those first three groupings were easy to make, as you can imagine. When placing fractions BETWEEN LANDMARKS, though, our generalizations became more advanced! Here we have two fractions that fall BETWEEN 0 and 1/2. In this case, the numerators are "less than half" of the denominators BUT "greater than zero".
Here we have two fractions that fall BETWEEN 0 and 1/2. In this case, the numerators are "less than half" of the denominators BUT "greater than zero".For example, with 2/6, half of 6 is 3, but fewer than 3 parts (only 2) are shaded; therefore, the fraction is LESS than 1/2.
Here we have three fractions that fall BETWEEN 1/2 and 1 whole. In this case, the numerators are "more than half" but "less than equal to" to denominator.
For example, half of 8 is 4, therefor 4/8 = 1/2.
If I have the fraction 5/8, since 5 is more than 4 (half the denominator), then the fraction is greater than 1/2.
We are now beginning to explore decimal and percent equivalents for fractions in class- new, powerful strategies to add to our tool belts when we compare fractions! Math is FUN when there are multiple ways to solve problems and justify our reasonings!
when there are multiple ways to solve problems and justify our reasonings!
 when there are multiple ways to solve problems and justify our reasonings!
when there are multiple ways to solve problems and justify our reasonings! What do you think about fractions, decimals, and percents? Leave a comment!
Love,
Mrs. Phillips


6 comments:
GREAT PICTURES!
Emma
FRACTIONS ARE SO COOL!!
Emma
I love fraction,decimals,and percents.I feel like I'm getting better and better.This has espesially helped me.
Chloe ML21
I sure wish this was the way I learned fractions in school. Your students are blessed to get this great conceptual basis.
I wish I was taught to better understand fractions when I was in elementary school. I just followed the steps but never understood why or how.
My children have a much better understanding of the concept at a much earlier age than I did thanks to the investigations they explored at Chets.
Thank you for giving them such a love for math. It's always a joy listening to them explain to me their thinking.
these fractions arevery good to learn from.
Post a Comment